crow

Utility library

---

Project maintained by CaptainCrowbar Hosted on GitHub Pages — Theme by mattgraham

Map Projections

Crow Library by Ross Smith

#include "crow/projection.hpp"
namespace Crow;

Contents

• Map Projections
  • Contents
  • Constants
  • Projection class overview
    • Class hierarchy
    • Map projection base class
    • Map projection template
    • Projection family intermediate base classes
  • Azimuthal projection classes
    • Azimuthal equidistant projection
    • Gnomonic projection
    • Lambert azimuthal projection
    • Orthographic projection
    • Stereographic projection
  • Cylindrical projection classes
    • Cylindrical equidistant projection
    • Gall-Peters projection
    • Lambert cylindrical projection
    • Mercator projection
  • Pseudo-cylindrical projection classes
    • Eckert IV projection
    • Mollweide projection
    • Sinusoidal projection
  • Interrupted projection classes
    • Interrupted Eckert IV projection
    • Interrupted Mollweide projection
    • Interrupted sinusoidal projection

Constants

enum class Maps: uint32_t;
std::string expand(Maps m);

Type used for bitmask flags.

Flag	Description
Maps::none = 0
	Projection family
Maps::azimuthal	Azimuthal projection
Maps::pseudoazimuthal	* Pseudo-azimuthal projection
Maps::conic	* Conic projection
Maps::pseudoconic	* Pseudo-conic projection
Maps::cylindrical	Cylindrical projection
Maps::pseudocylindrical	Pseudo-cylindrical projection
Maps::hybrid	* Hybrid projection
	Coverage of the globe
Maps::sub_hemisphere	Less than one hemisphere can be represented
Maps::hemisphere	One hemisphere can be represented
Maps::sub_sphere	More than one hemisphere, but less than the whole globe, can be represented
Maps::sphere	The complete globe can be represented
	Shape of the map
Maps::circle	The globe maps to a circle
Maps::ellipse	The globe maps to an ellipse
Maps::plane	The globe maps to an infinite plane
Maps::rectangle	The globe maps to a rectangle
Maps::square	* The globe maps to a square
Maps::other_shape	The globe maps to some shape not listed above
	Other properties
Maps::conformal	Local shape is preserved
Maps::equal_area	Area is preserved
Maps::hemisphere_circle	The hemisphere around the origin maps to a circle, making this suitable for paired hemisphere maps
Maps::interrupted	Interrupted projection
Maps::numerical	There is no analytic solution for globe_to_map(); the implementation uses Newton’s algorithm
	Masks
Maps::family_mask	Combination of all family bits
Maps::cover_mask	Combination of all coverage bits
Maps::shape_mask	Combination of all shape bits
Maps::other_mask	Combination of all other property bits

Bitmask constants. Each of these is a distinct one-bit bitmask. A projection’s map_properties constant (also reflected in its properties() function) is a combination of these values, indicating the properties of a specific projection. The properties bitmask of any given projection will contain exactly one bit from each of the first three groups, and any number of bits from the other properties group.

The expand() function breaks a bitmask down into its component values, e.g. "azimuthal|sphere|circle|hemisphere_circle".

Properties marked with a star are not actually used by any projection currently supported.

Projection class overview

Class hierarchy

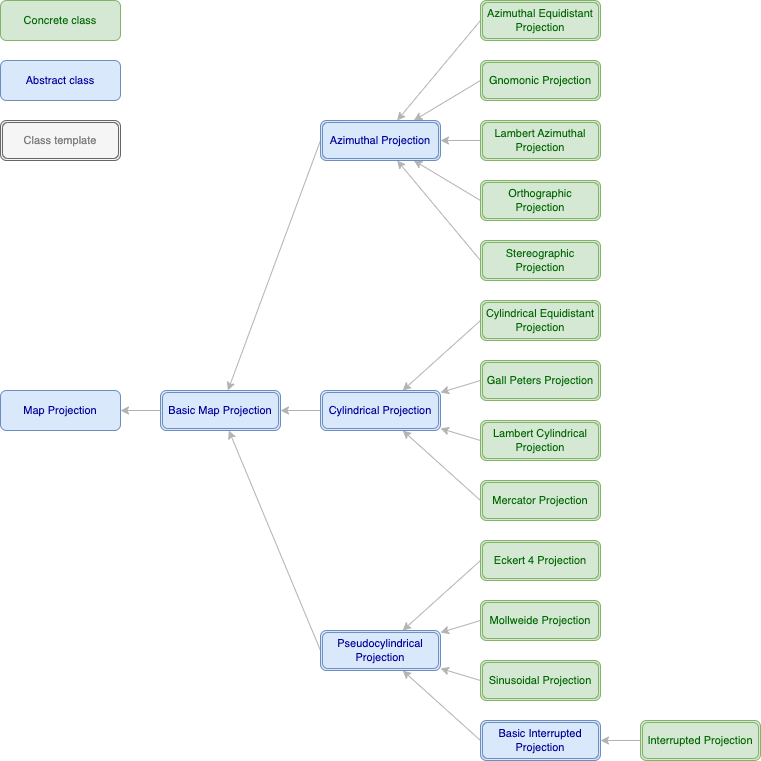
Map projection base class

class MapProjection

All map projection classes have this common base class, which provides properties that are independent of the scalar type used for coordinates.

virtual MapProjection::~MapProjection() noexcept;

Life cycle operations. All concrete projection classes are default constructible, copy and move constructible, and copy and move assignable (these functions are not explicitly documented for the concrete classes to avoid cluttering the documentation with repetitive boilerplate).

virtual std::string MapProjection::name() const;

The name of the projection.

virtual Maps MapProjection::properties() const noexcept;

The properties bitmask. This returns the same value as the concrete projection class’s map_properties constant, but is accessible through a base class reference.

Maps MapProjection::family() const noexcept;
Maps MapProjection::cover() const noexcept;
Maps MapProjection::shape() const noexcept;

These return the property flag from each property group. The value returned from each of these will always have exactly one bit set.

Map projection template

template <std::floating_point T> class BasicMapProjection: public MapProjection;

The common base class for all map projections with a specific scalar type.

using BasicMapProjection::value_type = T;
using BasicMapProjection::vector_type = Vector<T, 2>;

Member types.

static constexpr vector_type BasicMapProjection::default_origin = {0,π/2};

The default origin (centre point) for maps, the point where the prime meridian meets the equator, in spherical (φ,θ) coordinates.

virtual std::shared_ptr<BasicMapProjection>
    BasicMapProjection::clone() const;

Returns a copy of a projection object.

virtual bool BasicMapProjection::has_min_x() const noexcept;
virtual bool BasicMapProjection::has_max_x() const noexcept;
virtual bool BasicMapProjection::has_min_y() const noexcept;
virtual bool BasicMapProjection::has_max_y() const noexcept;
virtual T BasicMapProjection::min_x() const noexcept;
virtual T BasicMapProjection::max_x() const noexcept;
virtual T BasicMapProjection::min_y() const noexcept;
virtual T BasicMapProjection::max_y() const noexcept;

These indicate whether the map has a finite size in each direction, and if so, what the minimum and maximum values for x and y are. The max/min_[xy]() functions will return zero if the corresponding has_*() function is false. The has_*() functions do not normally need to be explicitly overridden, because for most projections they can be statically deduced from the properties bitmask.

The minimum values are currently redundant since all supported projection types are symmetrical about the origin; the functions are included to allow for future support of asymmetrical projections such as conic projections.

vector_type BasicMapProjection::globe_to_map
    (vector_type polar) const noexcept;
vector_type BasicMapProjection::map_to_globe
    (vector_type xy) const noexcept;

These provide the main functionality of a map projection class, converting in either direction between spherical (φ,θ) coordinates on the globe, and Cartesian (x,y) coordinates on the map. Results are unspecified (but not undefined) if the input point is not on the map (i.e. if is_on_globe(polar) or is_on_map(xy) is false, respectively).

bool BasicMapProjection::is_on_globe(vector_type polar) const noexcept;

Indicates whether a point on the globe’s surface (expressed as (φ,θ) spherical coordinates) is on the visible portion of the globe. For projections with the Maps::sphere property this will always be true.

bool BasicMapProjection::is_on_map(vector_type xy) const noexcept;

Indicates whether a point on the map (expressed as (x,y) Cartesian coordinates) is part of the projection of the globe.

vector_type BasicMapProjection::origin() const noexcept;

Returns the map’s centre point, expressed as (φ,θ) spherical coordinates. The φ coordinate supplied to the constructor will be reduced to the [0,2π) range; behaviour is undefined if the θ coordinate is negative or greater than π.

Projection family intermediate base classes

template <std::floating_point T> class AzimuthalProjection:
    public BasicMapProjection<T>;
template <std::floating_point T> class CylindricalProjection:
    public BasicMapProjection<T>;
template <std::floating_point T> class PseudocylindricalProjection:
    public BasicMapProjection<T>;

Base classes for specific families of projections. All projections currently implemented are derived from one of these; some of the infrastructure is in place to support other projection families such as conic projections, but no concrete projections of any other type are currently implemented.

Azimuthal projection classes

Azimuthal equidistant projection

template <std::floating_point T> class AzimuthalEquidistantProjection:
        public AzimuthalProjection<T> {
    static constexpr Maps map_properties =
        Maps::azimuthal | Maps::sphere | Maps::circle | Maps::hemisphere_circle;
    explicit AzimuthalEquidistantProjection(vector_type origin) noexcept;
};

Azimuthal equidistant projection, also known as the Postel or zenithal equidistant projection.

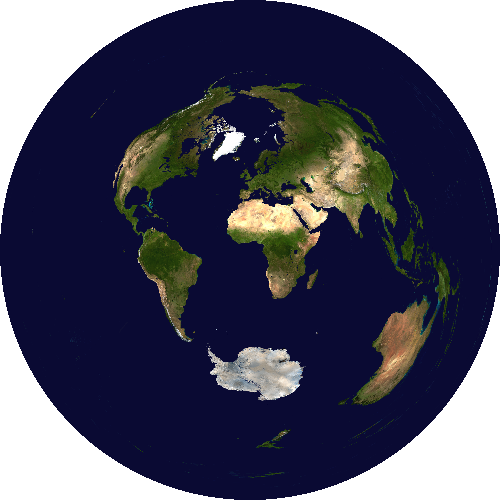
Gnomonic projection

template <std::floating_point T> class GnomonicProjection:
        public AzimuthalProjection<T> {
    static constexpr Maps map_properties =
        Maps::azimuthal | Maps::sub_hemisphere | Maps::plane;
    explicit GnomonicProjection(vector_type origin) noexcept;
};

Gnomonic projection.

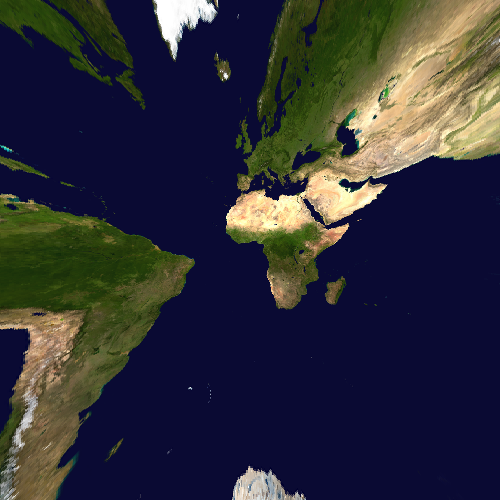
Lambert azimuthal projection

template <std::floating_point T> class LambertAzimuthalProjection:
        public AzimuthalProjection<T> {
    static constexpr Maps map_properties =
        Maps::azimuthal | Maps::sphere | Maps::circle | Maps::equal_area
        | Maps::hemisphere_circle;
    explicit LambertAzimuthalProjection(vector_type origin) noexcept;
};

Lambert azimuthal projection, also known as the azimuthal equal-area projection or Lambert zenithal equal-area projection.

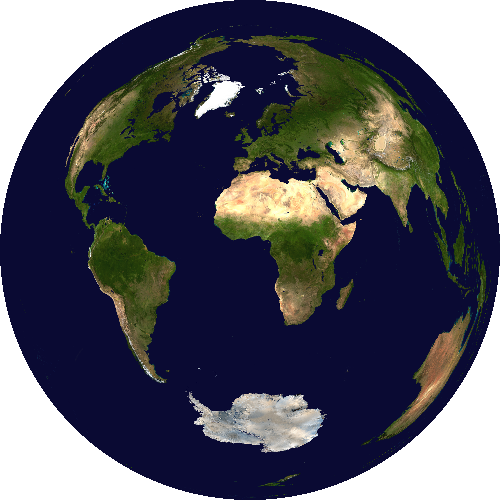
Orthographic projection

template <std::floating_point T> class OrthographicProjection:
        public AzimuthalProjection<T> {
    static constexpr Maps map_properties =
        Maps::azimuthal | Maps::hemisphere | Maps::circle
        | Maps::hemisphere_circle;
    explicit OrthographicProjection(vector_type origin) noexcept;
};

Orthographic projection, also known as the orthogonal projection.

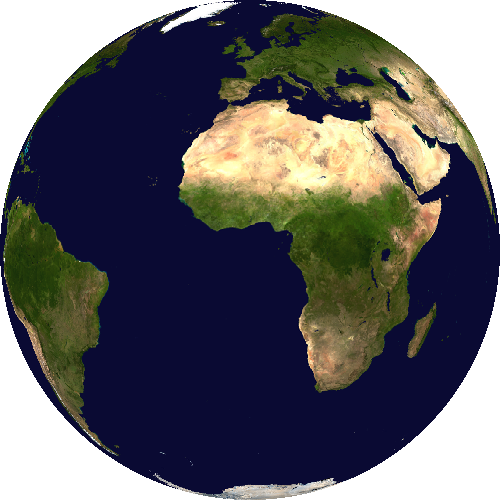
Stereographic projection

template <std::floating_point T> class StereographicProjection:
        public AzimuthalProjection<T> {
    static constexpr Maps map_properties =
        Maps::azimuthal | Maps::sub_sphere | Maps::plane | Maps::conformal
        | Maps::hemisphere_circle;
    explicit StereographicProjection(vector_type origin) noexcept;
};

Stereographic projection.

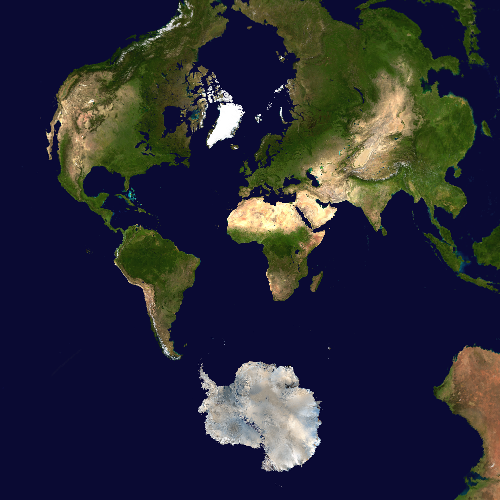
Cylindrical projection classes

Cylindrical equidistant projection

template <std::floating_point T> class CylindricalEquidistantProjection:
        public CylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::cylindrical | Maps::sphere | Maps::rectangle;
    explicit CylindricalEquidistantProjection(vector_type origin) noexcept;
};

Cylindrical equidistant projection, also known as the equirectangular projection, geographic projection, plate carrée projection, or simple cylindrical projection.

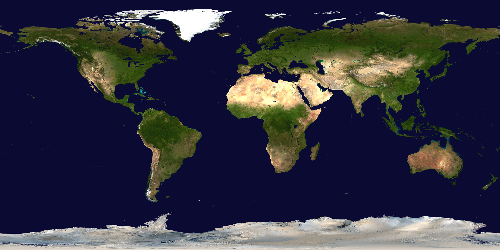
Gall-Peters projection

template <std::floating_point T> class GallPetersProjection:
        public CylindricalProjection<T> {
    static constexpr Maps map_properties =
        LambertCylindricalProjection<T>::map_properties;
    explicit GallPetersProjection(vector_type origin) noexcept;
};

Gall-Peters projection, also known as the Gall orthographic projection.

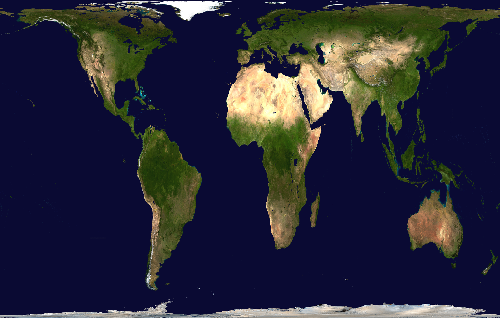
Lambert cylindrical projection

template <std::floating_point T> class LambertCylindricalProjection:
        public CylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::cylindrical | Maps::sphere | Maps::rectangle | Maps::equal_area;
    explicit LambertCylindricalProjection(vector_type origin) noexcept;
};

Lambert cylindrical projection, also known as the cylindrical equal-area projection.

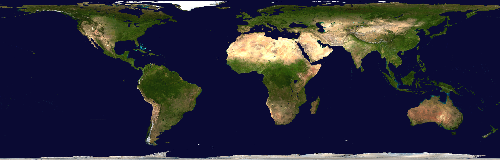
Mercator projection

template <std::floating_point T> class MercatorProjection:
        public CylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::cylindrical | Maps::sub_sphere | Maps::other_shape
        | Maps::conformal;
    explicit MercatorProjection(vector_type origin) noexcept;
};

Mercator projection.

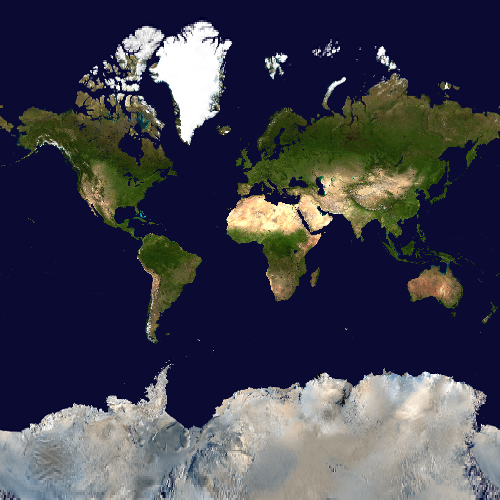
Pseudo-cylindrical projection classes

Eckert IV projection

template <std::floating_point T> class Eckert4Projection:
        public PseudocylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::pseudocylindrical | Maps::sphere | Maps::other_shape
        | Maps::equal_area | Maps::numerical;
    explicit Eckert4Projection(vector_type origin) noexcept;
};

Eckert IV projection.

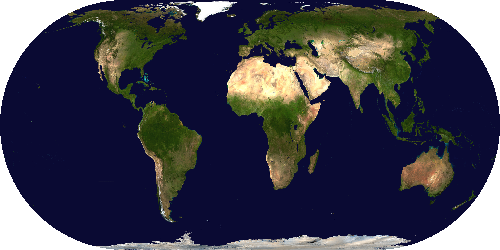
Mollweide projection

template <std::floating_point T> class MollweideProjection:
        public PseudocylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::pseudocylindrical | Maps::sphere | Maps::ellipse | Maps::equal_area
        | Maps::hemisphere_circle | Maps::numerical;
    explicit MollweideProjection(vector_type origin) noexcept;
};

Mollweide projection, also known as the Babinet projection, elliptical equal-area projection, or homolographic projection.

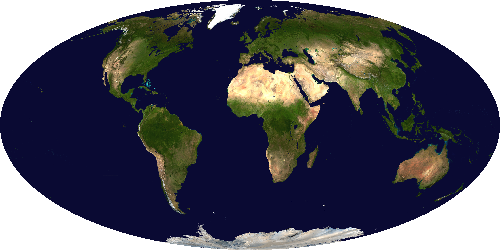
Sinusoidal projection

template <std::floating_point T> class SinusoidalProjection:
        public PseudocylindricalProjection<T> {
    static constexpr Maps map_properties =
        Maps::pseudocylindrical | Maps::sphere | Maps::other_shape
        | Maps::equal_area;
    explicit SinusoidalProjection(vector_type origin) noexcept;
};

Sinusoidal projection, also known as the Mercator equal-area projection or Sanson–Flamsteed projection.

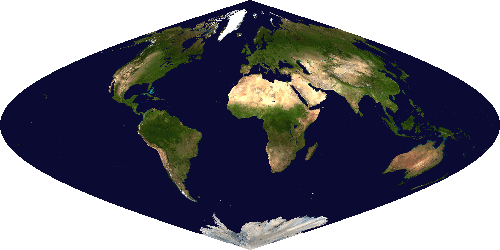
Interrupted projection classes

template <std::floating_point T> class BasicInterruptedProjection:
        public PseudocylindricalProjection<T> {
    template <RangeType Range> void interrupt(const Range& inter);
    template <RangeType Range> void interrupt(const Range& inter_north,
        const Range& inter_south);
};
template <typename Projection> class InterruptedProjection:
        public BasicInterruptedProjection<Projection::value_type> {
    using InterruptedProjection::projection_type = Projection;
    template <RangeType Range> InterruptedProjection(vector_type origin,
        const Range& inter);
    template <RangeType Range> InterruptedProjection(vector_type origin,
        const Range& inter_north, const Range& inter_south);
};

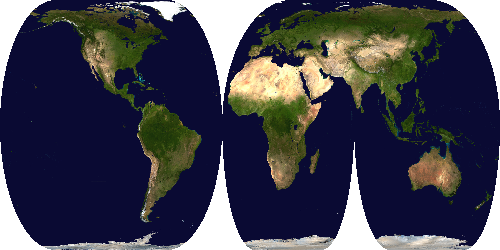
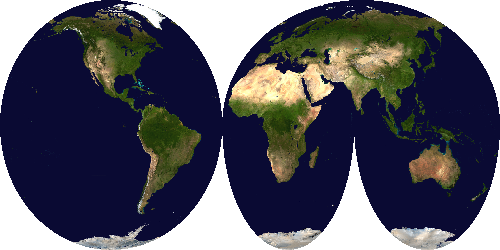
The InterruptedProjection class generates an interrupted version of a pseudo-cylindrical projection. The inter[_north/south] arguments supply a list of interruption points, expressed as φ coordinates (longitude), either for both hemispheres or for each hemisphere separately.

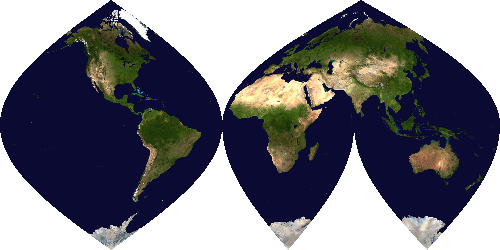
Interrupted Eckert IV projection

Interrupted Mollweide projection

Interrupted sinusoidal projection