crow

Utility library

---

Project maintained by CaptainCrowbar Hosted on GitHub Pages — Theme by mattgraham

Colour Space

Crow Library by Ross Smith

#include "crow/colour-space.hpp"
namespace Crow;

Contents

• Colour Space
  • Contents
  • Introduction
  • Supporting types
  • Colour space concepts
  • Colour space classes
    • List of classes
    • Relationship diagram
    • CIE colour spaces
      • CIE XYZ
      • CIE xyY
      • CIE L*a*b* and CIE L*u*v*
    • RGB colour spaces
      • RGB colour space templates
      • sRGB
      • Adobe RGB
      • ProPhoto
      • Wide Gamut
    • Polar colour spaces
      • CIE L*C*h colour spaces
      • HSL and HSV
    • Greyscale colour spaces
  • Functions
    • Conversion functions
    • Utility functions

Introduction

This documentation assumes that the reader is familiar with the basic concepts of colour theory. As a general rule of thumb, if you don’t know what colour space you should be using, you probably want LinearRGB for internal calculations (such as colour blending or interpolation), and sRGB for reading and writing image data. Your image I/O library may handle that conversion automatically, or it may require you to convert the colour space when reading or writing pixels.

The colour operations here are only defined for floating point channels, and are not intended to be called directly by users of this library. Refer to the Colour class for user-facing colour operations, on colours with integer or floating point channels.

As a simplification, I treat colour spaces as stateless. When the definition of a colour space includes state, such as a choice of standard illuminant or white point, this will need to be hardcoded into the colour space class, with different classes (probably template instantiations) for different parameters. See the WorkingSpace and NonlinearSpace templates below for examples.

Definitions of a colour space sometimes vary in the scaling of the coordinates. Here I use the unit range for CIE XYZ and closely related spaces, instead of the 0-100 range used in some sources, although I keep the 100-based scale for CIE L*a*b* and CIE L*u*v* since that is used universally.

For polar spaces such as HSL and HSV, I use a unit scale (i.e. a fraction of a circle) for the angular coordinate, instead of expressing it in radians or degrees. The polar coordinate is always first, and follows the usual convention in which the zero angle corresponds to red, and the angle increases in the red-to-yellow direction.

The term “working space” refers to the linear form of a nonlinear RGB space such as sRGB, before the transfer function (loosely called “gamma”) has been applied. The base space of a nonlinear space should be the corresponding working space, and the working space’s own base space should normally be CIE XYZ.

Bruce Lindbloom’s site is my main source for the RGB/XYZ matrices.

Supporting types

enum class Csp: int {
    none = 0,
    linear,  // Linear colour space
    polar,   // First channel is polar, not Cartesian
    rgb,     // Cartesian RGB-based colour space
    unit,    // Valid colours are restricted to the unit cube
};

Bitmask flags used to indicate the properties of a colour space. A linear colour space is one where operations like component-wise addition and scalar multiplication are well-defined.

Colour space concepts

template <typename CS> concept ColourSpace;

This checks the following requirements:

• Integer static member constant CS::count, indicating the number of channels in the colour space(not counting the alpha channel).
• Static member constant CS::channels, a std::array<char,CS::count> identifying each channel with a unique letter.
• Static member constant CH::properties, a bitmask of Csp values indicating the colour space’s properties.
• Member type CS::base, which is another colour space from which this one is defined. For the CIEXYZ space, the root of the colour space graph, CIEXYZ::base is itself. For all other colour space classes, the base must be another colour space that has already been defined. The dependency graph between colour spaces must be a directed acyclic graph, with no loops or disconnected subgraphs.
• Static member functions performing conversions between this space and its base space. The channel type T must be a floating point arithmetic type.
  • static Vector<T,CS::count> CS::from_base(Vector<T,CS::base::count> colour)
  • static Vector<T,CS::base::count> CS::to_base(Vector<T,CS::count> colour)

template <typename CS> concept LinearColourSpace;
template <typename CS> concept PolarColourSpace;
template <typename CS> concept RgbColourSpace;
template <typename CS> concept UnitColourSpace;

These match colour spaces with the appropriate properties.

Colour space classes

List of classes

Colour space	Base space	Properties	Description
CIEXYZ	CIEXYZ	linear,unit	CIE 1931 XYZ colour space
CIExyY	CIEXYZ	unit	CIE 1931 xyY colour space
CIELab	CIEXYZ	none	CIE 1976 L*a*b* colour space
CIELuv	CIEXYZ	none	CIE 1976 L*u*v* colour space
HCLab	CIELab	polar	CIE L*C*hab colour space
HCLuv	CIELuv	polar	CIE L*C*huv colour space
sRGB	LinearRGB	rgb,unit	Standard sRGB colour space
LinearRGB	CIEXYZ	linear,rgb,unit	Linear RGB working space for sRGB
AdobeRGB	LinearAdobeRGB	rgb,unit	Adobe RGB (1998) colour space
LinearAdobeRGB	CIEXYZ	linear,rgb,unit	Working space for Adobe RGB
ProPhoto	LinearProPhoto	rgb,unit	ProPhoto (ROMM RGB) colour space
LinearProPhoto	CIEXYZ	linear,rgb,unit	Working space for ProPhoto
WideGamut	LinearWideGamut	rgb,unit	Adobe Wide Gamut (opRGB) colour space
LinearWideGamut	CIEXYZ	linear,rgb,unit	Working space for Wide Gamut
HSL	LinearRGB	polar,unit	Polar transformation of linear RGB
HSV	LinearRGB	polar,unit	Polar transformation of linear RGB
Greyscale	CIEXYZ	linear,unit	Greyscale
sGreyscale	Greyscale	unit	Gamma adjusted greyscale

Relationship diagram

Arrows point from each colour space to its base space.

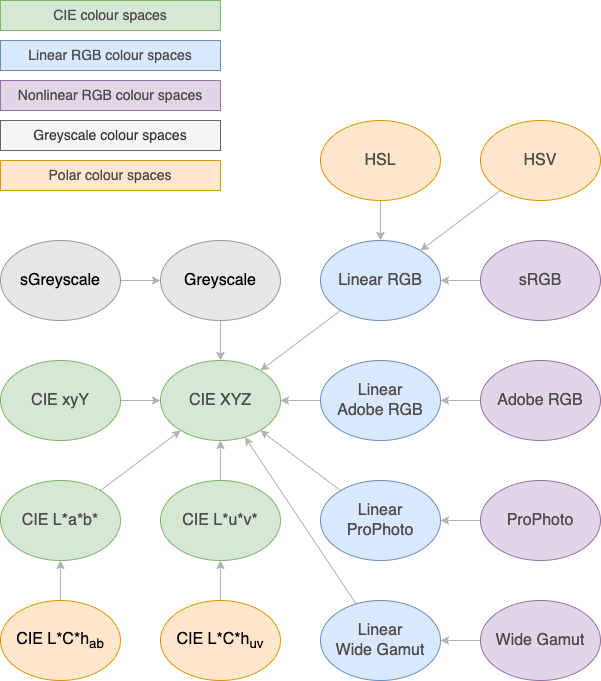
CIE colour spaces

CIE XYZ

class CIEXYZ {
    using base = CIEXYZ;
    static constexpr std::array<char, 3> channels = { 'X', 'Y', 'Z' };
    static constexpr Csp properties = Csp::linear | Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept { return colour; }
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept { return colour; }
};

CIE 1931 XYZ colour space.

CIE xyY

class CIExyY {
    using base = CIEXYZ;
    static constexpr std::array<char, 3> channels = { 'x', 'y', 'Y' };
    static constexpr Csp properties = Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

CIE 1931 xyY chromaticity-based colour space.

CIE L*a*b* and CIE L*u*v*

class CIELab {
    using base = CIEXYZ;
    static constexpr std::array<char, 3> channels = { 'L', 'a', 'b' };
    static constexpr Csp properties = Csp::none;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};
class CIELuv {
    using base = CIEXYZ;
    static constexpr std::array<char, 3> channels = { 'L', 'u', 'v' };
    static constexpr Csp properties = Csp::none;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

CIE 1976 L*a*b* and L*u*v* colour spaces.

RGB colour spaces

RGB colour space templates

template <int64_t M00, int64_t M01, int64_t M02,
    int64_t M10, int64_t M11, int64_t M12,
    int64_t M20, int64_t M21, int64_t M22,
    int64_t Divisor>
class WorkingSpace {
    using base = CIEXYZ;
    static constexpr std::array<char, 3> channels = { 'R', 'G', 'B' };
    static constexpr Csp properties = Csp::linear | Csp::rgb | Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

Template for a generic linear RGB working space. The template arguments are the elements of the RGB to XYZ conversion matrix, expressed as integer ratios, in row major order (e.g. the top left entry is M00/Divisor).

template <typename WorkingSpace,
    int64_t GammaNumerator, int64_t GammaDenominator>
class NonlinearSpace {
    using base = WorkingSpace;
    static constexpr std::array<char, 3> channels = { 'R', 'G', 'B' };
    static constexpr Csp properties = Csp::rgb | Csp::unit;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

Template for a generic nonlinear RGB colour space that uses a simple exponent (gamma) for the transfer function. The gamma value is equal to GammaNumerator/GammaDenominator. Colour spaces that use nontrivial transfer functions (such as sRGB) will need to be individually defined instead of using this template.

sRGB

using LinearRGB = WorkingSpace<...>;
class sRGB {
    using base = LinearRGB;
    static constexpr std::array<char, 3> channels = { 'R', 'G', 'B' };
    static constexpr Csp properties = Csp::rgb | Csp::unit;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

The widely used sRGB standard colour space, and its linear working space.

Adobe RGB

using LinearAdobeRGB = WorkingSpace<...>;
using AdobeRGB = NonlinearSpace<LinearAdobeRGB, 22, 10>;

Adobe RGB (1998) colour space, and its linear working space.

ProPhoto

using LinearProPhoto = WorkingSpace<...>;
class ProPhoto {
    using base = LinearProPhoto;
    static constexpr std::array<char, 3> channels = { 'R', 'G', 'B' };
    static constexpr Csp properties = Csp::rgb | Csp::unit;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

ProPhoto (a.k.a. ROMM RGB) colour space, and its linear working space.

Wide Gamut

using LinearWideGamut = WorkingSpace<...>;
using WideGamut = NonlinearSpace<LinearWideGamut, 563, 256>;

Adobe Wide Gamut (a.k.a. opRGB) colour space, and its linear working space.

Polar colour spaces

CIE L*C*h colour spaces

template <typename Base> class HCLSpace {
    using base = Base;
    static constexpr std::array<char, 3> channels = { 'H', 'C', 'L' };
    static constexpr Csp properties = Csp::polar;
    template <ArithmeticType T> static Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};
using HCLab = HCLSpace<CIELab>;
using HCLuv = HCLSpace<CIELuv>;

CIE L*C*h_ab and L*C*h_uv colour spaces. These are simply the L*a*b* and L*u*v* colour spaces expressed in polar coordinates (as usual, the polar channel H is expressed on a 0-1 scale, but L is still 0-100 and C is unbounded). These follow the usual rule that the polar channel comes first; both orders (LCH or HCL) can be observed in the wild.

HSL and HSV

class HSL {
    using base = LinearRGB;
    static constexpr std::array<char, 3> channels = { 'H', 'S', 'L' };
    static constexpr Csp properties = Csp::polar | Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};
class HSV {
    using base = LinearRGB;
    static constexpr std::array<char, 3> channels = { 'H', 'S', 'V' };
    static constexpr Csp properties = Csp::polar | Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 3> colour) noexcept;
};

Polar transformations of linear RGB.

Greyscale colour spaces

class Greyscale {
    using base = CIEXYZ;
    static constexpr std::array<char, 1> channels = { 'Y' };
    static constexpr Csp properties = Csp::linear | Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 1>
        from_base(Vector<T, 3> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 3>
        to_base(Vector<T, 1> colour) noexcept;
};
class sGreyscale {
    using base = Greyscale;
    static constexpr std::array<char, 1> channels = { 'Y' };
    static constexpr Csp properties = Csp::unit;
    template <ArithmeticType T> static constexpr Vector<T, 1>
        from_base(Vector<T, 1> colour) noexcept;
    template <ArithmeticType T> static constexpr Vector<T, 1>
        to_base(Vector<T, 1> colour) noexcept;
};

One-dimensional colour spaces. The single channel in the Greyscale space is simply the Y channel from CIE XYZ. The sGreyscale channel is the linear greyscale after applying the sRGB transform to make it more visually uniform.

Functions

Conversion functions

template <ColourSpace CS1, ColourSpace CS2, ArithmeticType T>
    Vector<T, CS2::count> convert_colour_space(Vector<T, CS1::count> colour);

Converts between any two colour spaces, passing through any intervening base spaces along the way, by chaining the colour spaces’ to_base() and from_base() functions.

Utility functions

For any function that takes a scale argument, behaviour is undefined if scale<=0.

template <ColourSpace CS, ArithmeticType T>
    constexpr bool is_colour_in_gamut(Vector<T, CS::count> colour,
        T scale = 1) noexcept;

True if the colour is in gamut for the colour space. For unit-cube or unit-polar spaces, this checks that all channels are in the range [0,scale] (or [0,scale) for the polar channel); for non-unit polar spaces, it just checks that the polar channel is in range. For other spaces, this has nothing to check and always returns true.

template <ColourSpace CS, ArithmeticType T>
    constexpr void clamp_colour(Vector<T, CS::count>& colour,
        T scale = 1) noexcept;

Clamps the channel values where necessary to ensure that the colour is in gamut. For polar spaces, the first channel is reduced modulo scale, yielding a value in the range [0,scale). Unit channels (all channels for unit-cube spaces, and all but the first channel for unit-polar spaces) are clamped to the range [0,scale]. For unbounded spaces, and for all but the first channel in non-unit polar spaces, this does nothing.